Neural Differential Equations
for Timeseries Forecasting
in Julia
by Stephan Sahm
founder of Jolin.io IT consulting

Stephan Sahm

  • Founder of Jolin.io
  • Full stack data science consultant
  • Applied stochastics, uncertainty handling
  • Big Data, High Performance Computing and Real-time processing
  • Making things production ready

Jolin.io

  • We are based in Munich, working for Europe
  • We focus on Julia consulting, high performance computing, machine learning and data processing.
  • We build end-to-end solutions, including data architecture, MLOps, DevOps, GDPR, user interface, ...
  • 10+ years experience in Data Science
    5+ years in IT consulting
    5+ years with Julia
Julia User Group Munich
Julia Computing
MI4People MI4People
Machine Learning Reply
Economy for the common good

Outline

Julia Introduction
Differential Equations within Neural Nets
Neural Nets within Differential Equations
Uncertainty Learning - Bayesian Estimation and DiffEq
Symbolic Regression
Benchmarks

Julia introduction

  • Developed and incubated at MIT
  • Just had 10th anniversary
  • Version 1.0 in 2018
  • Generic programming language
  • Focus on applied mathematics
  • Alternative to Python, R, Fortran, Matlab

3 Revolutions at once

30x-300x faster than Python
All in 1 language
Multimethods instead of inheritance simplify code-reuse and maintenance

Where is Julia used in production?

Industries Pharma, Energy, Finance, Medicine & Bio-technology
Fields of application Modeling/simulation, optimization/planning, Data Science, High Performance Computing, Big Data, Real-time

Multimethods

intuitive generic programming - every function is an interface

Method specialization works for arbitrary many arguments as well as if types and functions are in different packages

Mandel-brot Example

Julia 30x faster than Python & Numpy

100% Julia versus mixture Python & C

Python
Time:
1000x1000 in 4.5 min (267 sec)
200x200 in 10 sec

Optimising Python is generally depending on performant packages like Numpy & Numba.

better performance
=
better usage of performant packages

Julia
Time:
1000x1000 in 9 sek
200x200 in 0.4 sek

Optimising Julia can be done everywhere.

better performance
=
better usage of Julia itself

Differential Equations within Neural Nets

Example Lotka-Volterra equations:
Dynamics of population of rabbits and wolves.
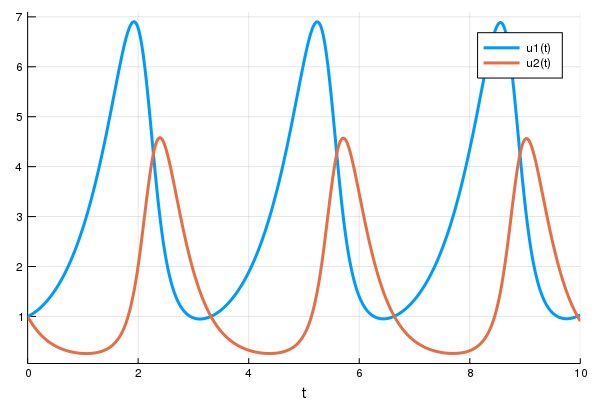
$$ x^\prime = \alpha x - \beta x y $$ $$ y^\prime = -\delta y + \gamma x y $$

Julia model
Solving and plotting

Source: https://julialang.org/blog/2019/01/fluxdiffeq/

Putting ODE into Neural Network Framework Flux.jl

loss function (let's say we want a constant number of rabbits)

train for 100 epochs

can be part of larger network

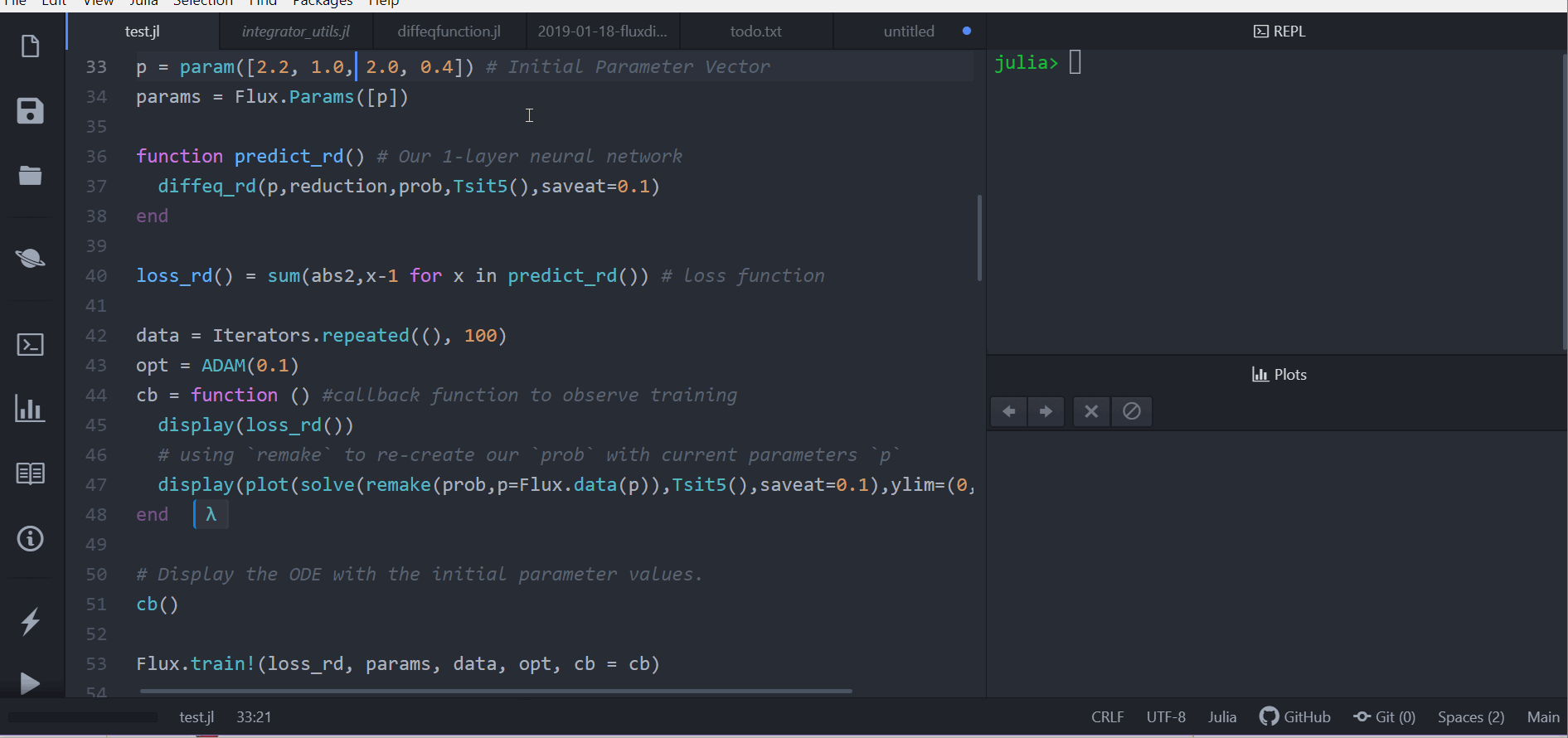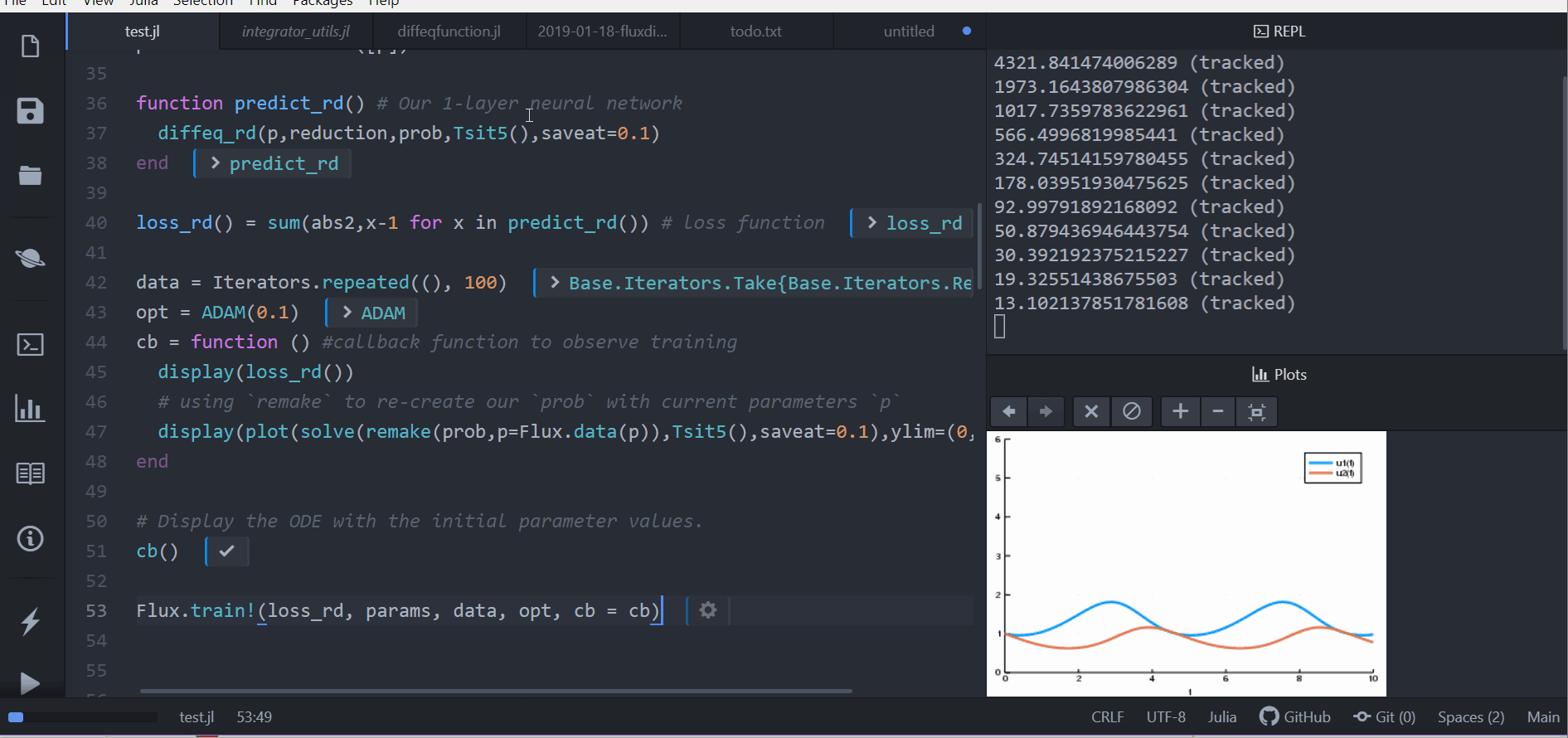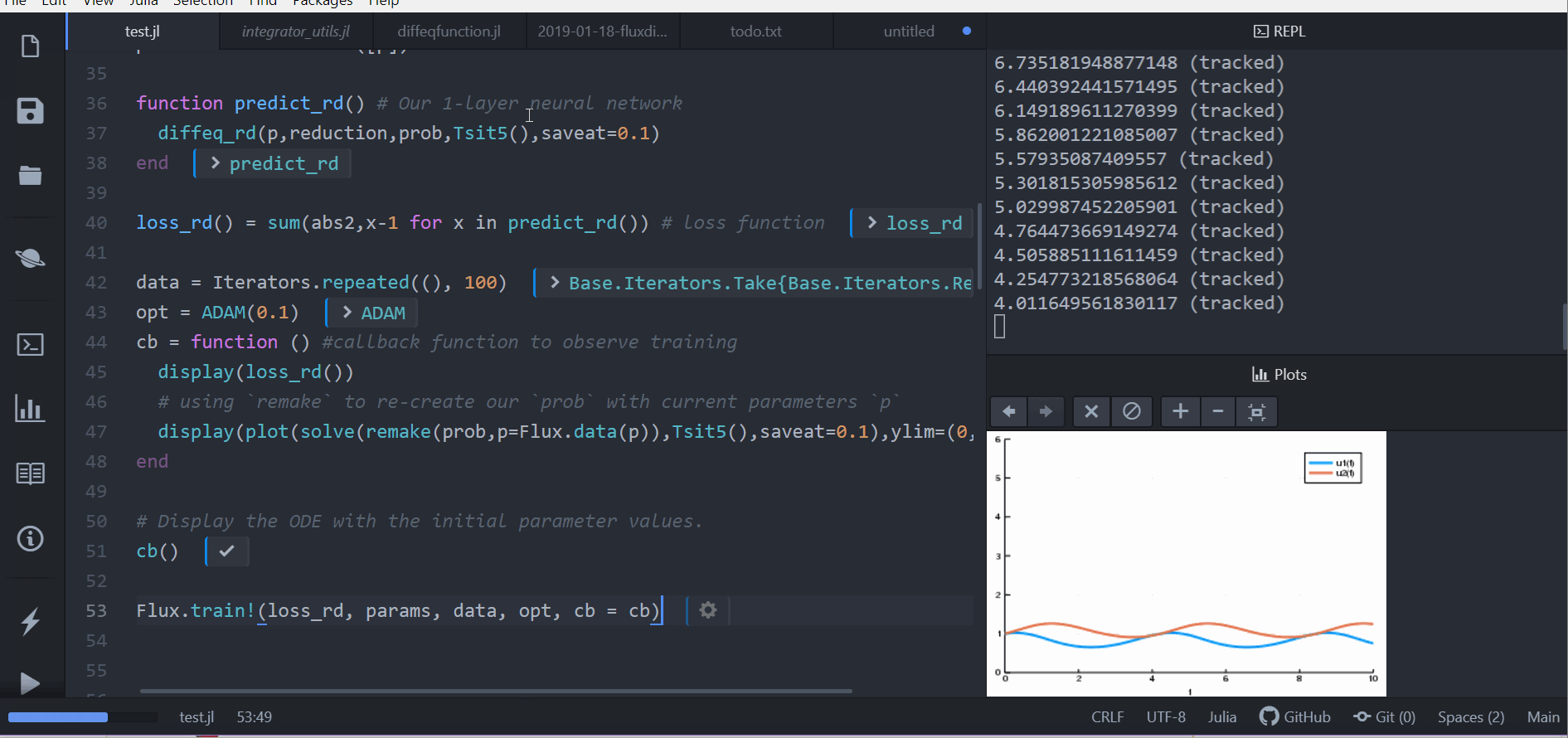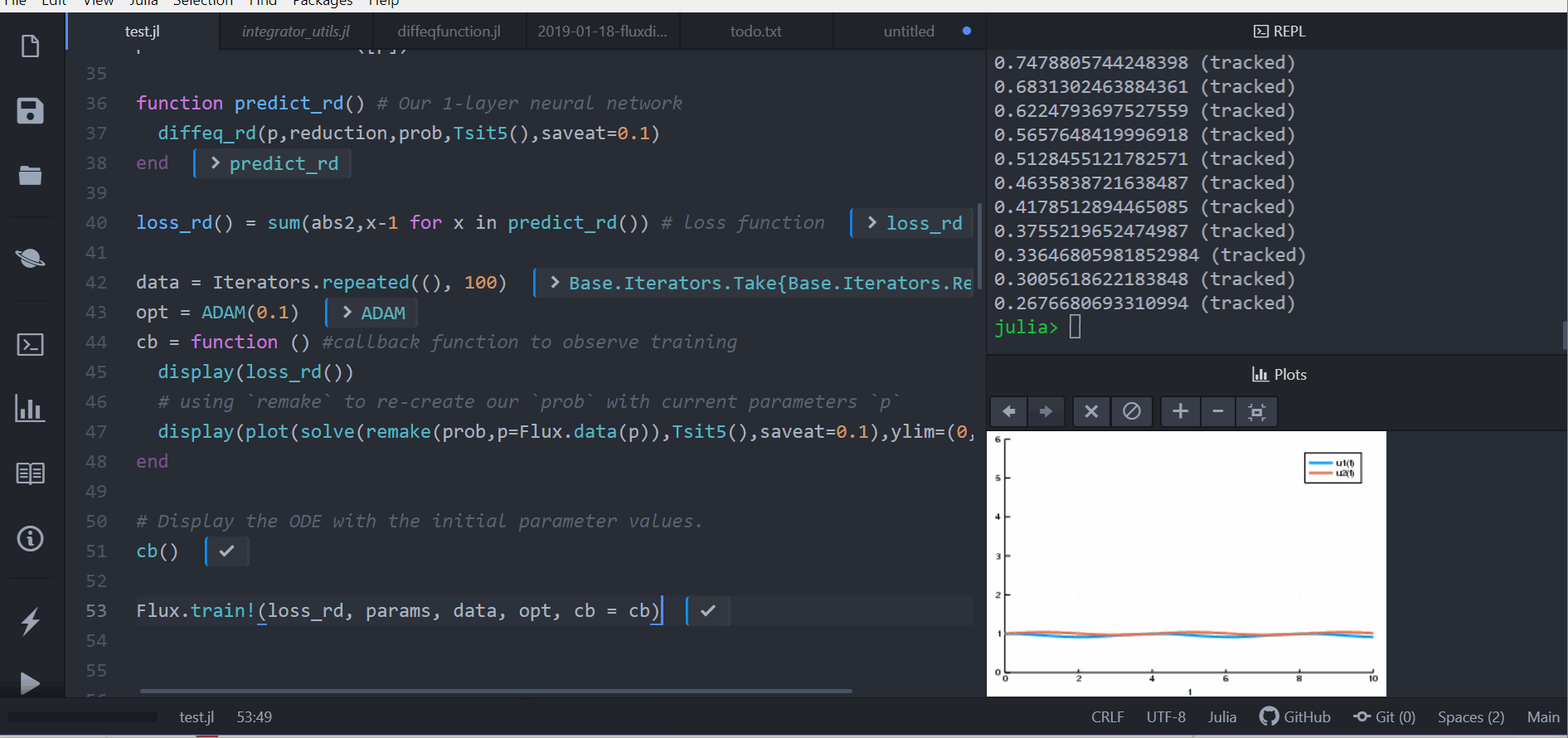
Neural Nets within Differential Equations

Ground Truth $u^\prime = A u^3$

Model $u^\prime$ with neural network.
(multilayer perceptron with 1 hidden layer and a tanh activation function)

Source: https://julialang.org/blog/2019/01/fluxdiffeq/

plot

train

Neural Nets within Differential Equations

Alternative motivation for Neural Differential Equations: Generalization from Residual Nets.

Source: Neural Ordinary Differential Equations (Chen et al. 2019)

Residual Neural Network
discrete difference layers

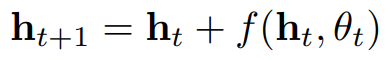
Neural Ordinary Differential Equation

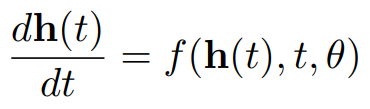
Uncertainty Learning - Bayesian Estimation and DiffEq

Let's assume noisy data

Let's assume we only have predator-data (wolves)

Probabilistic Model of the parameters

Source: https://turing.ml/dev/tutorials/10-bayesian-differential-equations/

Sample & plot

Symbolic Regression

DataDrivenDiffEq.jl

Extract human readable formula from learned Neural Differential Equation

Benchmarks

Source: Universal Differential Equations for Scientific Machine Learning (Rackauckas et al. 2021)

Features

Speed

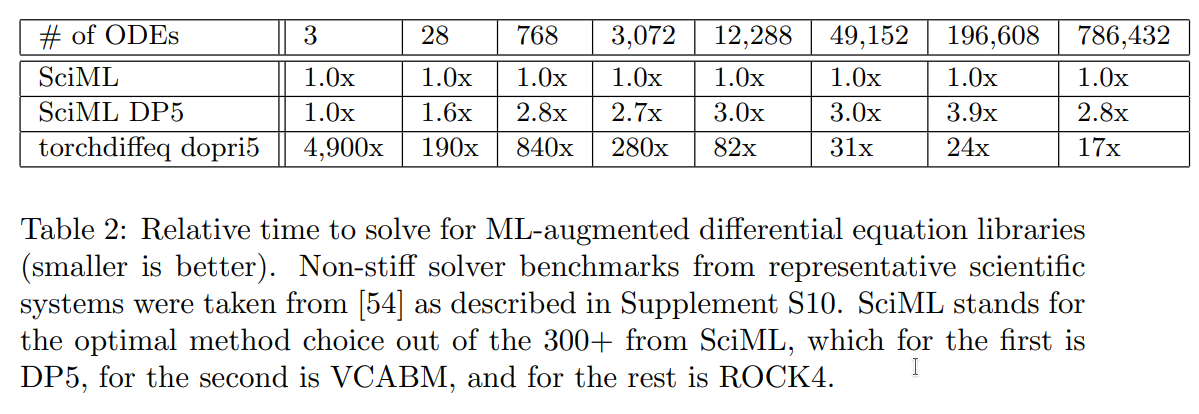
“torchdiffeq’s adjoint calculation diverges on all but the first two examples due to the aforementioned stability problems.”

tfdiffeq (TensorFlow equivalent): “speed is almost the same as the PyTorch (torchdiffeq) code base (±2%)”

Summary

Julia Introduction
  • 30x-300x faster than Python
  • 100% Julia
  • Multimethods
Differential Equations within Neural Nets
  • Think of an ODE as another layer for your Neural Network.
  • Works with ODE, SDE, DDE, DAE, PDE.
Neural Nets within Differential Equations
  • Model the derivative with a Neural Network.
  • Generalization of Residual Networks.
  • Works with ODE, SDE, DDE, DAE, PDE.
Uncertainty Learning - Bayesian Estimation and DiffEq
  • Model randomness.
  • Capture training uncertainty.
  • Works with ODE, SDE, DDE, DAE, PDE.
Symbolic Regression
  • Extract human readable formulas.
Benchmarks
  • Widest range of features.
  • Highest speed, especially for problems with viewer parameters.

Thank you for your interest

I am happy to answer all your questions. Please reach out to me or Jolin.io.

jolin.io consulting

hello@jolin.io
+49 152 2406 7803
linkedin.com/company/jolin-io
www.jolin.io